subject to s.t. 约束为
最优化问题= 目标函数+约束函数
运筹学里的一种
无约束优化/约束优化
线性/非线性优化 目标函数+约束函数有非线性函数
连续优化（股票投资比例）/离散优化 （如整数规化：路径选择、生产车辆）
单目标优化/多目标优化（考虑多个方面，比如租房）
动态规划
随机规划
鲁棒优化
无约束最优化问题
GD
梯度下降法：结束的两个条件
- 梯度小于预设的精度
- 迭代之间的x足够接近
- 轮次已经达到，超时
缺陷：局部最优，而非全局最优
Newton Method
原函数具有二阶连续偏导数；
一阶偏导=0，二阶偏导>0，记二阶偏导（海塞矩阵为Hx)
不断地求最小值，迭代公式为x^{k+1}=x^{k}-H_{k}^{-1}*f’(x^k)
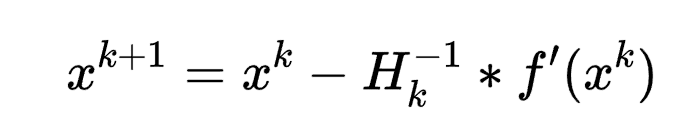
缺陷：求解海塞矩阵的逆矩阵求解过程比较复杂。
quasi拟牛顿法
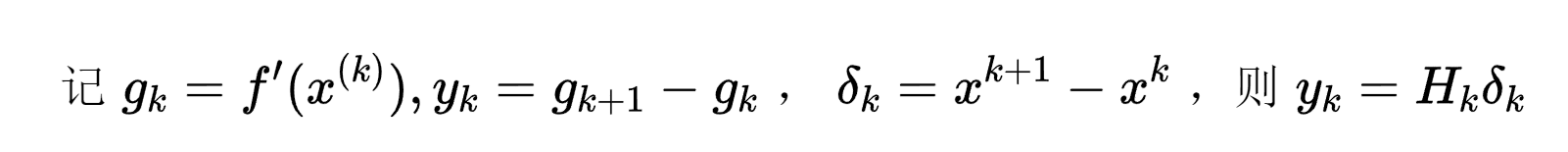
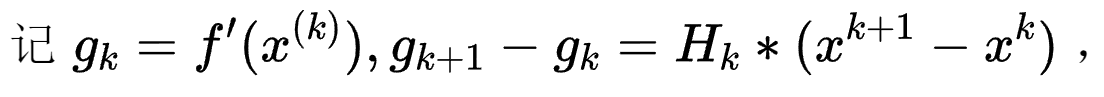
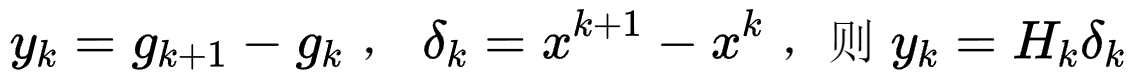
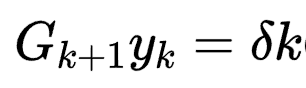拟牛顿条件。
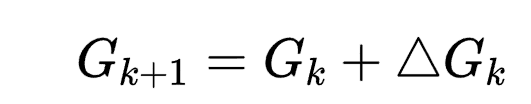
选择Gk作为海塞矩阵逆的近似。
DFP算法
Davidon-Fletcher-Powell
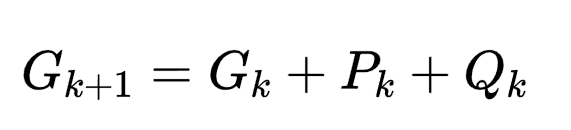
其中，令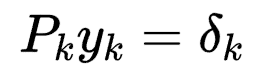
，则可求出用Gk表示的Pk，Qk，进而得到Gk的迭代公式。
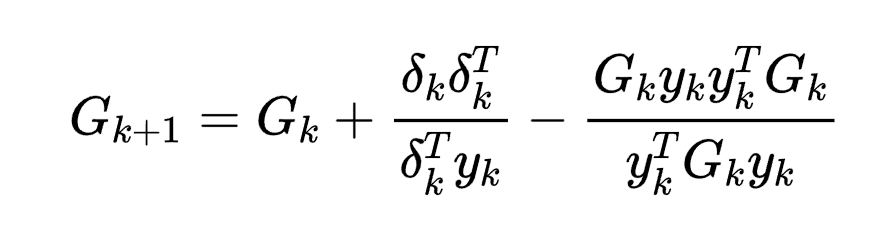
BFGS
Broyden-Fletcher-Goldfarb-Shanno
和DFP算法相似，只是从Gk换为了Bk,拟牛顿条件：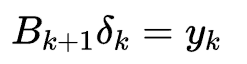
，迭代的构造为：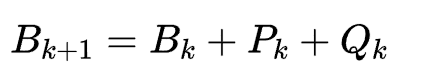
。
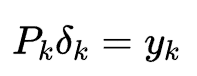SMO
序列最小优化算法，Sequential minimal optimization
SMO是一种解决此类支持向量机优化问题的迭代算法。由于目标函数为凸函数，一般的优化算法都通过梯度方法一次优化一个变量求解二次规划问题的最大值，但是，对于以上问题，由于限制条件
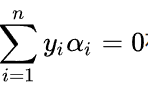存在，当某个a_i从a_iold更新到a_inew时，述限制条件即被打破。为了克服以上的困难，SMO采用一次更新两个变量的方法。