学习策略:间隔最大化。形式化为一个凸二次规划(convex quadratic programming)问题,等价于正则式的合页损失函数的最小化问题。
由简到繁:
- 线性可分——>学习线性的分类器——>线性可分(硬间隔)支持向量机;
- 数据近似线性可分—>软间隔最大化—>学习线性的分类器—>线性支持向量机;
- 数据线性不可分—>kernel trick+软间隔最大化—>非线性支持向量机(等价于在高维空间中学习线性支持向量机);
1.超平面:

2.函数间隔和几何间隔
因为超平面wx+b=0,所以对于点(xi,yi),(wxi+bi)能够表示点距离超平面的远近,其与yi的乘积的符号可以用来表示分类的正确性(-1表示分类错误,分类正确时)。
所以ri=yi(wxi+bi)定义为超平面关于样本点(xi,yi)的函数间隔;超平面关于训练集T的函数间隔为所有超平面关于每个样本点的函数间隔的最小值。
r’=min(ri)
函数间隔规范化(确保超平面不变的时候,间隔也是确定的)后,即w=w/||w||,b=b/||w||,函数间隔r'变为几何间隔r。
约束优化问题为:求解能够正确划分训练数据集并且使得几何间隔最大的分离超平面。
约束:正确划分训练数据集==任意样本的距离大于最小距离==yi(w/||w||·xi+b/||w||) >=r== yi(w·xi+b) >=r'
求解:max几何间隔r==max {r’/||w||} ,由于w和b可以等比例放缩,所以可令r’=1,此时最优化问题为调整w和b以最大化1/||w||,在约束条件y_i(w·x_i+b) ≥1下,而该式等价于下面的凸二次规划(convex quadratic programming)问题求解
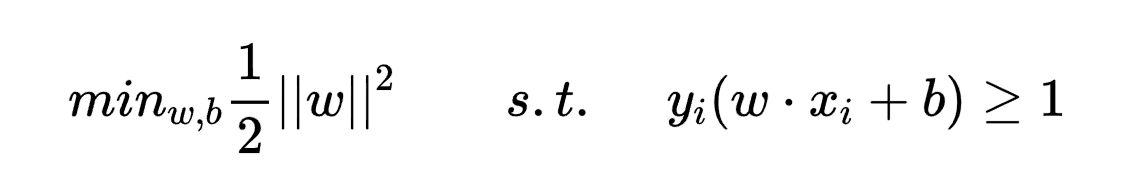
上面的式子即为最大间隔法的算法实现。
之所以构造成二次规划问题,是为了方便之后的求导。
3.间隔最大化
学习算法思想:让几何间隔最大化,即max r ,以足够确信对超平面周围的点正确分类,通过求解上个分段的最优化问题,解得超平面(w*,b*)。
由此得到分类决策函数为f(x)=sign(w*x+b*)1.支持向量
4.支持向量
在线性可分情况下才存在。两个类别中距离分离超平面最近的样本。即对于支持向量(xi,yi),yi(w·xi+b) =1,或者说yi(w·xi+b) -1=0,它们构造出来两个超平面(w·xi+b)±1=0,记这两个超平面为H1和H2。
由于移动两个边界以外的样本对解无影响,而移动支持向量解会发生变化,所以支持向量非常重要。
5.对偶问题
·genralized lagrange uality
原始约束最优化问题转化为广义拉格朗日函数的极小极大(min max L(x,α,β))问题,在KKT条件(导数值=0,对偶互补条件满足,原来的条件满足,拉格朗日乘子>=0)下,原始问题和对偶问题的最优值相等,此时,去解对偶问题的最优解。
附录
内积

完备性就是说任意柯西列的极限仍然在这个空间中。
完备的内积空间称为希尔伯特空间。它是欧几里德空间(距离、内积、向量所具有的线性性质)的一个推广,其不再局限于有限维的情形。或者,如果一个空间是线性的,完备的,并且规定了范数,内积和距离的,就叫做希尔伯特空间。

向量的长度叫做模,将模的概念推广,只要满足正定性、齐次性和三角不等式的映射就叫做范数。
L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)
L1范数是指向量中各个元素绝对值之和
L2范数是指向量各元素的平方和然后求平方根,通常意义的模长。
凸优化
若二阶导数在区间上非负,则称为凸函数
若二阶导数在区间上恒大于0,则称严格凸函数
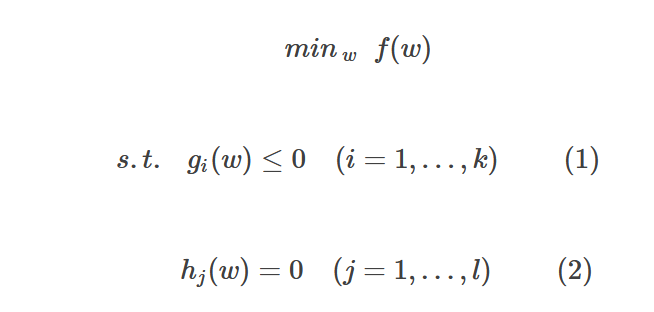
假设f、g、h在定义域内是连续可微的,且目标函数f和不等式约束函数g是凸函数,等式约束h是仿射函数(线性函数),则约束最优化问题称为凸优化问题。
开发技巧
SVM+poly核函数+degree=1,相当于线性SVM。
SVM在标准化后的数据上效果好
linear有上限,开始即巅峰,巅峰即退役;而rbf可调参数多,训练速度快,可能性大。
