1.准则函数
把要最小化或最大化的函数称为目标函数(objective function)或准则(criterion)。
当对其进行最小化时,我们也把它称为代价函数(cost function)、损失函数(loss function)或误差函数(error function)。
- Classification Error(分类错误率) 错误分类占比
- Mean Squared Error (均方误差),
- Cross Entropy Loss Function(交叉熵损失函数)
Loss Func可以用来判断模型在样本上的表现;
1.1 Mean Squared Error (均方误差),

前提是估计噪声服从高斯分布

缺点就是其偏导值在输出概率值接近0或者接近1的时候非常小,这可能会造成模型刚开始训练时,偏导值几乎消失。导致模型在一开始学习的时候速率非常慢,而使用交叉熵作为损失函数则可以避免这样。
1.2 交叉熵损失函数(Cross Entropy Loss Function)
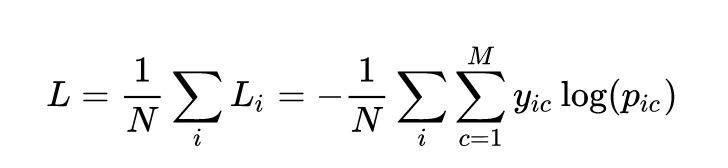
M分类的N个样本:对于每个样本i,计算各个分类标签yic与标签概率pic的log值的积的和值。计算出的L是正数,L越小,模型的表现越好。
1 | from sklearn.metrics import log_loss |
2.最大熵模型
参考b站课程
MaxiMum Entropy model:所有可能的概率分布中,熵最大的是最好的。
模型首先满足约束条件, 对于不确定的部分假定其等可能,所以等概率表示了对于事实的无知。

定义:

最大熵模型: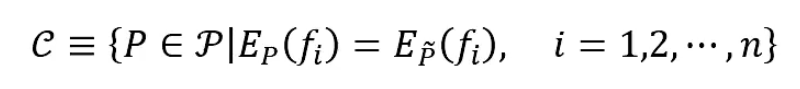
找出C中条件熵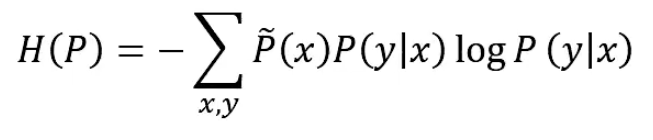 最大的模型。
最大的模型。
形式化为最优化问题,求等价的约束下最小值:
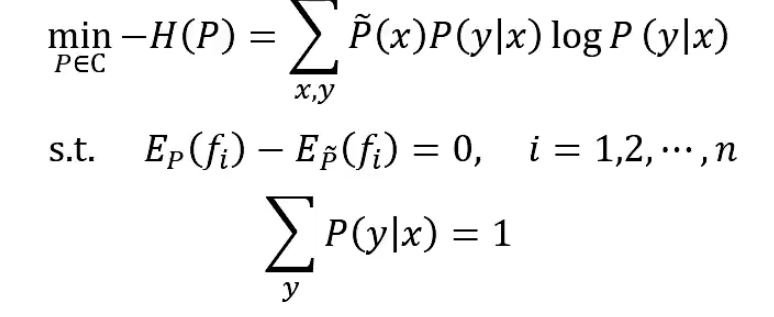
引进拉格朗日乘子w0,w1,…,wn,定义拉格朗日函数L(P,w)。将约束最优化问题转换为无约束最优化的对偶问题。
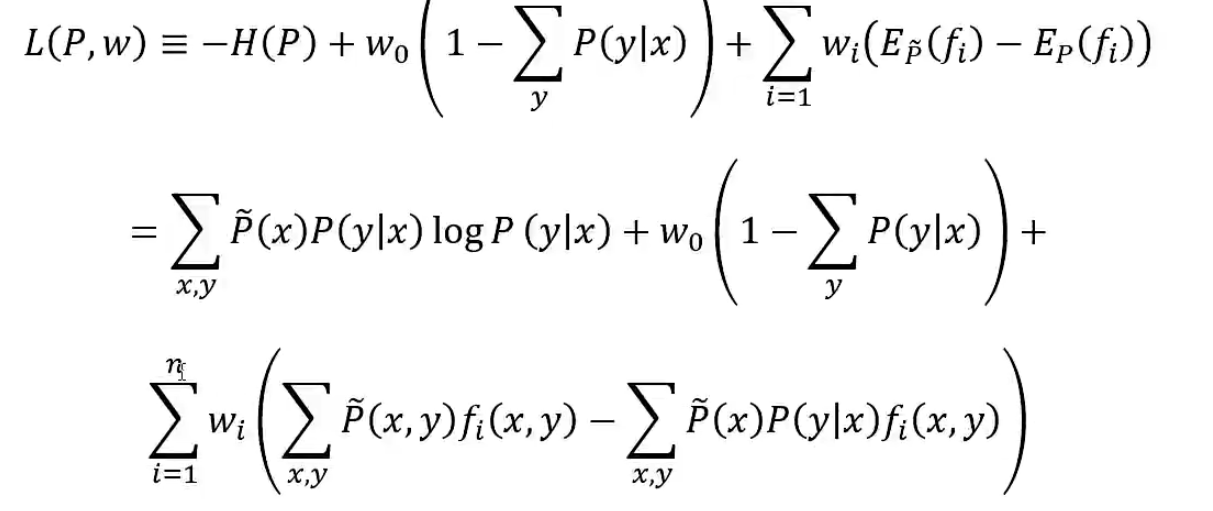
最优化的原始问题:
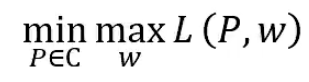
它的对偶问题:
通过求解对偶问题找到原始问题的解:
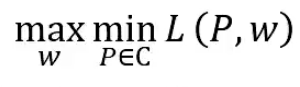
对偶函数的极大化等价于最大熵模型的极大似然估计,其证明部分请参考视频43min以后内容。这里不做记录。
先求出最小的拉格朗日函数L(P,w),再对其求最大值。


举例使用
设Y有5个取值,A,B,C,D,E,估计取各个值的概率。
P(A)+P(B)+P(C)+P(D)+P(E)=1
P(A)+P(B)=3/10
以y1,y2,…,y5分别表示A~E,得到最大熵模型学习的最优化问题:
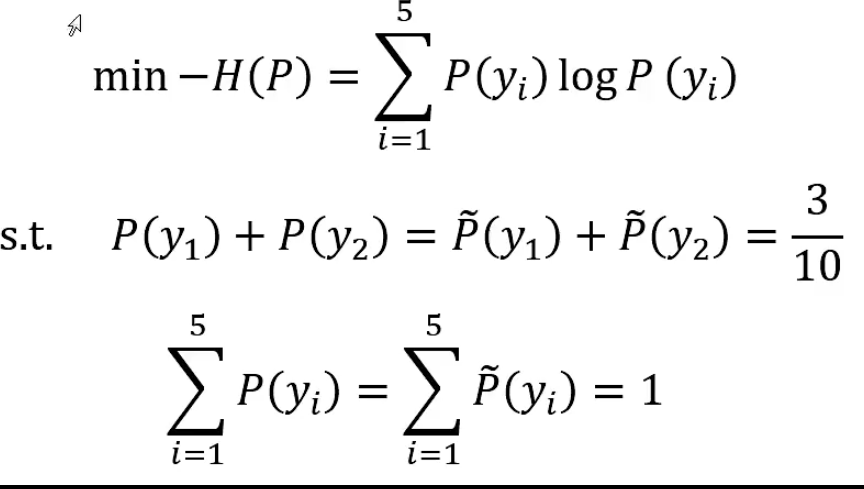
定义拉氏函数
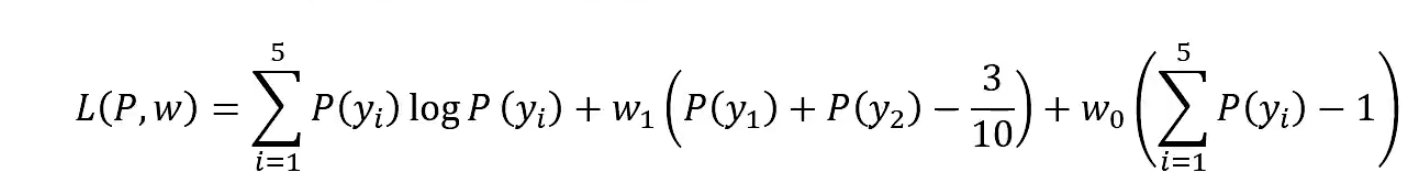
求偏导:
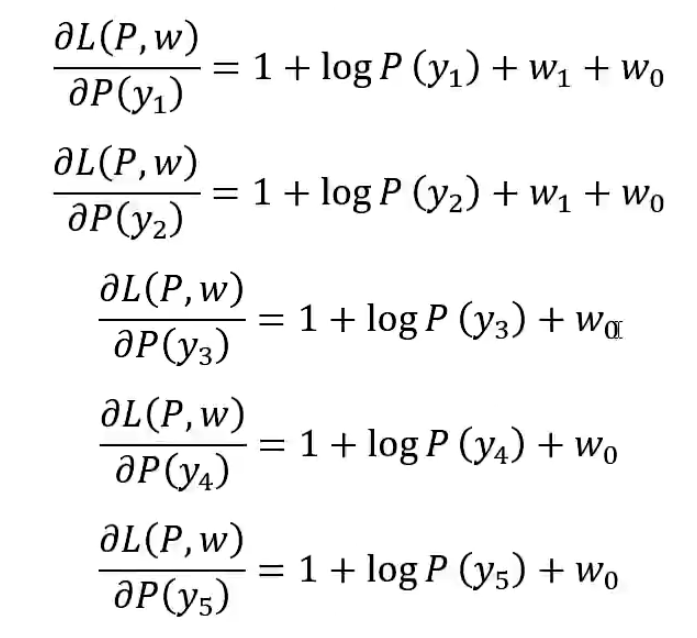 (*)
(*)
令各个偏导为0,解得P(y1)~P(y5)
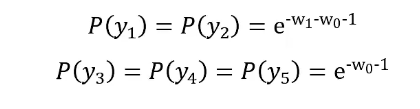 ,代入拉格朗日式子里,
,代入拉格朗日式子里,
得到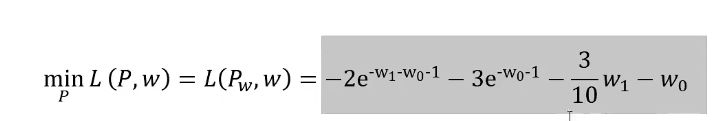
再求解上式关于w的极大化问题:
对上式分别用w0,w1求偏导,并令其导数为0.得到w0和w1后,将其带回*式得到最终的P(y0)~p(y5)。
可以证明,等概率时,熵也是最大的。